10654. Уникальный цвет

 

Дано дерево с n вершинами, пронумерованными от 1 до n. i - ое ребро соединяет вершину ai и вершину bi. Вершина i окрашена в цвет ci (в этой задаче цвета представлены целыми числами).

Вершина x  считается хорошей, если кратчайший путь от вершины 1 до вершины x не содержит вершину, окрашенную в тот же цвет, что и вершина x, кроме самой вершины x.

Найдите все хорошие вершины.

 

Вход. Первая строка содержит количество вершин n (2 ≤ n ≤ 105). Вторая строка содержит цвета c1, c2, ..., cn (1 ≤ ci ≤ 105). Каждая из следующих n – 1 строк содержит два целых числа ai и bi (1 ≤ ai, bi ≤ n).

 

Выход. Выведите все хорошие вершины в виде целых чисел в порядке возрастания. Каждое число следует выводить в отдельной строке.

 

Пример входа 1

Пример выхода 1

6

2 7 1 8 2 8

1 2

3 6

3 2

4 3

2 5

1

2

3

4

6

 

 

Пример входа 2

Пример выхода 2

10

3 1 4 1 5 9 2 6 5 3

1 2

2 3

3 4

4 5

5 6

6 7

7 8

8 9

9 10

1

2

3

5

6

7

8

 

 

РЕШЕНИЕ

графы – поиск в глубину

 

Анализ алгоритма

Запустим поиск в глубину из вершины 1. При входе в вершину v цвета color[v] увеличим значение used[color[v]] на 1. Значение used[color[v]] содержит количество раз, которое вершина цвета color[v] встретилась на пути от 1 до v (включая саму вершину v). Если цвет color[v] на пути встретился только один раз, то вершина v хорошая, заносим ее в результирующее множество.

При выходе из вершины v значение used[color[v]] следует уменьшить на 1.

 

Пример

Граф из первого примера имеет вид:

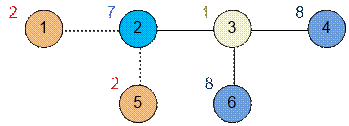
Вершина 5 не является хорошей, так как на пути 1 – 2 – 5 вершины 5 и 1 имеют одинаковый цвет.

Вершина 6 является хорошей, так как на пути 1 – 2 – 3 – 6 цвета вершин отличны от цвета вершины 6.

 

Реализация алгоритма

Входной граф храним в списке смежности g. Объявим рабочие массивы.

 

vector<int> used, color;

vector<vector<int>> g;

set<int> st;

 

Функция dfs реализует поиск в глубину. Переменная par является предком v.

 

void dfs(int v, int par)

{

 

Вершина v имеет цвет color[v]. Отмечаем, что на пути из вершины 1 встретилась вершина цвета color[v].

 

  used[color[v]]++;

 

Значение used[color[v]] содержит количество раз, которое вершина цвета color[v] встретилась на пути от 1 до v (включая саму вершину v). Если цвет color[v] на пути встретился только один раз, то вершина v хорошая, заносим ее в результирующее множество st.

 

  if (used[color[v]] == 1) st.insert(v);

 

Перебираем все ребра (v, to), исходящие из v. Если to не является предком v (to ≠ par) то запускаем из to поиск в глубину. При этом предком to становится v.

 

  for (int to : g[v])

    if (to != par) dfs(to, v);

 

При выходе из вершины v уменьшаем значение used[color[v]] на 1.

 

  used[color[v]]--;

}

 

Основная часть программы. Читаем количество вершин n и массив цветов.

 

scanf("%d", &n);

color.resize(n + 1);

for (i = 1; i <= n; i++)

  scanf("%d", &color[i]);

 

Читаем граф.

 

used.resize(100001);

g.resize(n + 1);

for (i = 1; i < n; i++)

{

  scanf("%d %d", &x, &y);

  g[x].push_back(y);

  g[y].push_back(x);

}

 

Запускаем поиск в глубину из вершины 1.

 

dfs(1, 1);

 

Выводим хорошие вершины. Они содержатся во множестве st.

 

for (int val : st)

  printf("%d\n", val);